CCF A类会议 ICLR2025论文:Noise-DA模型论文学习笔记
论文原文
前置知识
降噪
跨域问题
扩散模型
背景
真实物理环境下图像的噪声恢复,噪声如:雨、雾、噪点(噪点的产生也受到物理世界中的时间影响)
核心难点
物理世界下,照片中的时间维度无法复现。导致数据集难以构建标签。解决方法可解耦为两部分:
数据集构建:通过标签y伪造输入x以获取数据集(x,y) 。
模型设计:跨域问题引出的一系列方法,如,无监督学习、半监督学习、对比学习等。
研究现状
跨域研究
像素空间伪造
特征空间伪造
作者首次提出噪声空间的伪造
模型设计
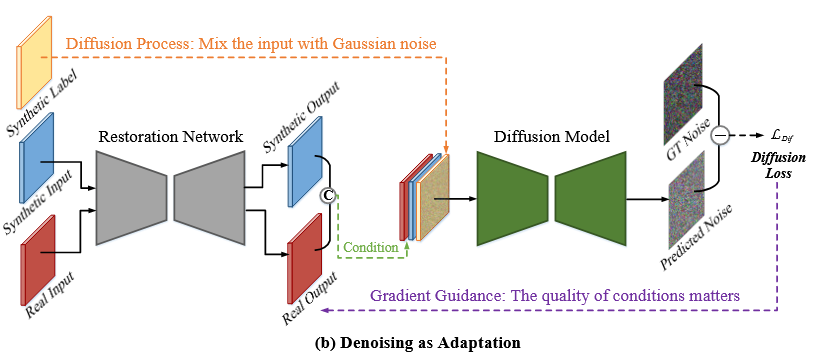
可以分为一个恢复模型(网络)和扩散模型。
恢复模型做的就是简单的图生图,没有别的模块。
扩散模型实现的真实域和伪造域的融合,这里甚至不要求真实图像和伪造图像有任何关系。
扩散模型输入的三个通道介绍:
扩散模型目标是预测噪声,这个噪声是我们在模型输入层特意引入的一个高斯噪声通道。
另外两个通道是真实域数据的输出和伪造域数据的输出
这块可以参考🔌老师的回复:
🧩 一、普通扩散模型在做什么
扩散模型是一种逐步去噪的生成模型。
它的目标是:从随机噪声恢复出干净图像。Step 1:加噪(forward process)
我们先拿一张干净图像y,逐步加噪,直到完全变成高斯噪声:
q(\tilde{y}_t|y) = \sqrt{\bar{\alpha}_t},y + \sqrt{1-\bar{\alpha}_t},\epsilon, \quad \epsilon \sim \mathcal{N}(0, I)所以\tilde{y}_t是加噪的图像。
Step 2:去噪(reverse process)
训练一个神经网络 \epsilon_\theta(\tilde{y}_t, t),让它学会预测出噪声 \epsilon。
它的训练目标是:L = E_{y,t,\epsilon}\big[|\epsilon - \epsilon_\theta(\tilde{y}_t, t)|^2\big]也就是说——
扩散模型不是直接生成图像,而是“猜出加进去的噪声”是多少。
一旦模型能准确预测噪声,就能反向一步步“去掉噪声”,从而生成干净图像。
🧠 二、在本文中的角色:作为“教师”指导恢复网络
在这篇论文里,扩散模型不再是生成图像的主角,而是变成一个评估者(teacher / critic)。
它仍然执行“预测噪声”这个任务,但其输入被特别设计来实现“域对齐(domain adaptation)”。模型输入与输出:
损失函数:
L_{Dif} = E\big[|\epsilon - \epsilon_\theta(\tilde{y}_s | C(\hat{y}_s, \hat{y}_r), t)|^2\big]
这里\epsilon是我们加噪时用的“真实噪声”,
\epsilon_\theta是扩散模型的预测,
目标是让两者接近。
🔍 三、那为什么这样能“指导恢复网络”?
这是关键直觉:
如果条件 C(\hat{y}_s, \hat{y}_r)(也就是恢复网络输出的图像)更接近真实干净分布,
那扩散模型就能更准确地预测噪声。换句话说:
扩散模型本身“知道什么是干净图像”(它学过 clean distribution);
当恢复网络输出的结果(condition)比较干净时,它的噪声预测误差更小;
所以我们用扩散模型的噪声预测误差来“奖励”恢复网络。
于是恢复网络的目标变成:
生成那种能让扩散模型更容易预测噪声的图像。
也就是——输出更符合干净图像分布的结果。
⚙️ 四、总结成一句话
扩散模型通过噪声预测误差间接告诉恢复网络:
“你输出的结果离干净图像分布有多远。”
✅ 一句话总结:
扩散模型的任务仍然是“预测噪声”,但在这篇论文里,它不再用来生成图像,而是作为一个“分布判别器”,通过噪声预测误差来引导恢复网络的输出在合成域与真实域之间对齐到干净域。